Authors:
(1) Ankit Anand, Department of Physics, Indian Institute of Technology Madras, Chennai 600 036, India;
(2) Ruben Campos Delgado, Bethe Center for Theoretical Physics, Physikalisches Institut der Universit¨at Bonn, Nussallee 12, 53115 Bonn, Germany.
Table of Links
2 Modified Einstein equations with the Jacobson’s approach
3 Quantum gravitational corrections to the Schwarzschild metric
3 Quantum gravitational corrections to the Schwarzschild metric
In order to solve (2.9), we start with the Ansatz
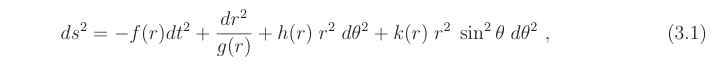
where
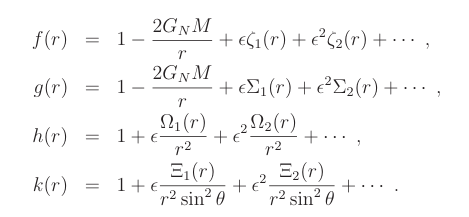
The Ricci scalar has the structure


Case I
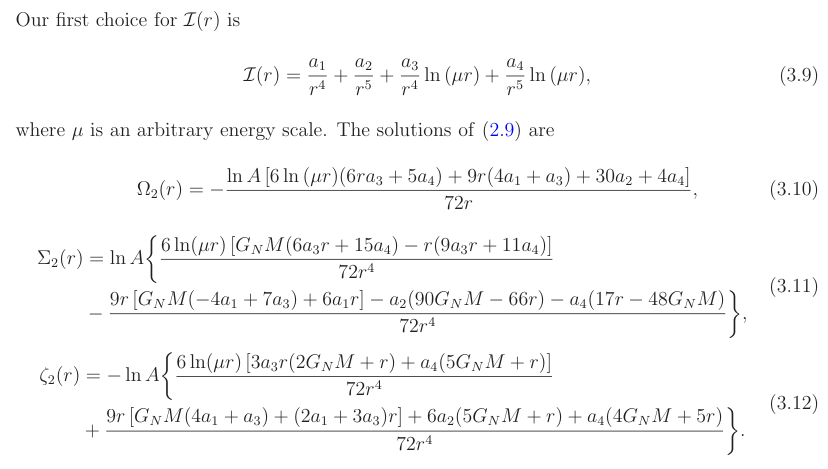
We compare our solutions with the ones of Xiao and Tian [32], which read
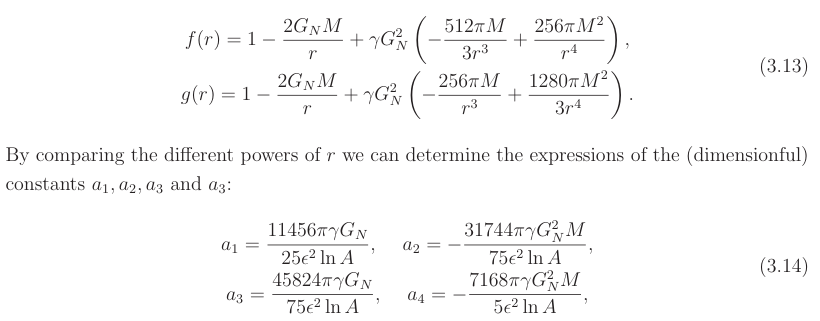
With all these terms the final expression for the metric is

which generalizes the result of [32]. Notice that the coefficients (3.14) are formally divergent, but the solutions (3.15)-(3.17) are finite.
Case II
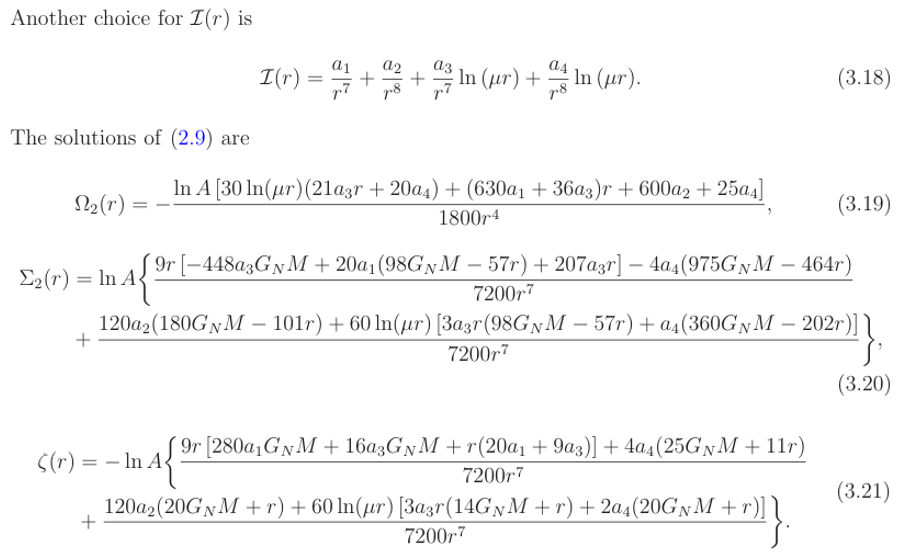
We compare now our solutions with the ones of Calmet and Kuipers, [22], which read
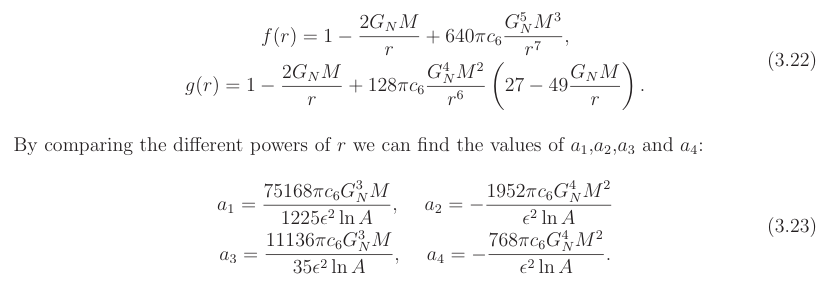
With all these terms the final expression for the metric is
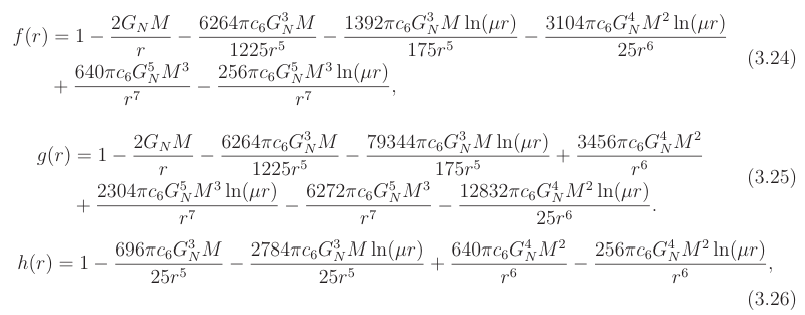
hich generalizes the result of [22]. Again, notice that the coefficients (3.23) are formally divergent, but the solutions (3.24)-(3.26) are finite.
This paper is available on arxiv under CC BY 4.0 Deed license.

