Authors:
(1) Ankit Anand, Department of Physics, Indian Institute of Technology Madras, Chennai 600 036, India;
(2) Ruben Campos Delgado, Bethe Center for Theoretical Physics, Physikalisches Institut der Universit¨at Bonn, Nussallee 12, 53115 Bonn, Germany.
Table of Links
2 Modified Einstein equations with the Jacobson’s approach
3 Quantum gravitational corrections to the Schwarzschild metric
Abstract

1 Introduction
Black holes are intriguing entities for several reasons. Hawking’s discovery that black holes have a radiation spectrum comparable to that of a black body gives them a perfect laboratory for studying the interactions between quantum mechanics, gravity, and thermodynamics. The concept of Bekenstein-Hawking entropy, often known as black hole entropy, has gained popularity in recent decades. The exploration of black hole entropy is essential for gaining insights into the intricate microscopic aspects of quantum gravity. The renowned Bekenstein–Hawking entropy, which is proportional to the area of the horizon, represents a foundational expression [1,2] in this realm. However, within the broader context of quantum gravity, this entropy is regarded merely as the tree-level outcome of black hole entropy, with subsequent refinements revealing a leading-order quantum gravitational correction in the form of a logarithmic term. This logarithmic correction is deemed fundamental and universal due to its derivation from diverse methods. These approaches encompass conical singularity and entanglement entropy [2,3], Euclidean action method [4–7], conformal anomaly [8], Cardy formula [9], quantum tunneling [10, 11], and quantum geometry [12]. This ubiquity underscores the significance of the logarithmic correction in our comprehension of black hole entropy.
The exploration of black hole entropy is fundamental to grasp the intricate nature of the microscopic constituents within the framework of quantum gravity. One of the most renowned expressions in this realm is the Bekenstein-Hawking entropy, denoted as
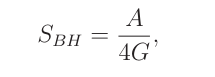
where A is the event horizon area of the black hole. This formula represents a pivotal link between the geometric properties of black holes, such as their event horizon area, and the underlying quantum structure, providing invaluable insights into the nature of spacetime at the smallest scales. The Bekenstein-Hawking entropy differs from conventional thermodynamics in that it is proportional to the black hole horizon area instead of the volume. In classical thermodynamics, a system entropy is proportional to its mass and volume, indicating an extensive and additive quantity. However, the cause for black hole entropy being nonextensive is unknown [13]. Based on the Bekenstein-Hawking entropy, there are several developments of alternative construction based on nonextensive statistics, such as Renyi [14] and Tsallis [15]. Recent studies on entropy include Barrow’s entropy [16], Sharma-Mittal’s [17], and Kaniadakis’ [18, 19]. The first law of thermodynamics links entropy, temperature, internal energy, and heat transport. Changing the definition of entropy can affect these other numbers, as in [20].
As we don’t yet have a complete theory of quantum gravity that works for all energy scales, using effective field theory (EFT) techniques on general relativity gives us a reliable theory of quantum gravity up to an energy scale near the Planck scale [21]. By applying EFT methods, we can recognize certain common aspects of quantum gravity. One of the most fascinating features is the dynamic non-locality of space-time caused by quantum effects when we look at very short distances. Quantum corrections are expected to adjust the black hole metric to match the corrected entropy since it is calculated by the black hole horizon area and event horizon radius. The starting point for the EFT approach is a curvature expansion from which equations of motion can be derived. Previous studies found that the metric of a Schwarzschild black hole acquires quantum corrections at the third level of curvature [22], while the metric of a Reissner-Nordstrom black hole receives modifications already at second order [23]. The authors employed the same strategy to derive a revised geometry and corrected entropy using the Wald formula [24], despite various methods available [25–28].

This paper is available on arxiv under CC BY 4.0 Deed license.

